1. If the cost price of cello pen is 90% of the selling price. Find the profit or loss percent?
A. 11.11%
B. 35.45%
C. 48.34%
D. 15.82%
E. None of these
Solutions
⇒ Let selling price of pen be 100
∴ cost price of pen = 100 × (90/100) = 90Profit percentage = [(100 – 90)/90] × 100 = 11.11%
2. The discount offered on a product is 20%. If the profit on that product is 27.5%, find the cost price. Given that the marked price of the product is Rs. 637.50.
A. Rs. 400
B. Rs. 500
C. Rs. 540
D. Rs. 575
E. Rs. 475
Solutions
Given that,
Marked price = 637.5 Rs
∴ Selling price = 80% of 637.5 ⇒ 510
Let the cost price be Rs. x
127.5/100 x = 510
∴ x = 400
∴ Cost price of product is = 400
Short Trick:
Required Cost Price = (637.5 × 0.8)/127.5 × 100
⇒ 400 Rs
3. Rakesh sold sofa set for Rs. 22,500 with a discount of 20% and loss 10%. If no discount is offer, what is the condition for Rakesh?
A. 12.5% loss
B. 10.5% profit
C. 10.5% loss
D. 15% profit
E. None of the above
Solutions
Discounted Price – Rs. 22,500
% of discount offer = 20%
% of loss = 10%
Selling Price = (100 – % of discount) × Marked price
⇒ 22500 = 80% of marked price
⇒ marked price = 22500/0.80 = Rs. 28125
For cost price,
Loss = Cost price – selling Price
Consider, cost price as Rs. x,
% of loss always consider by cost price,
⇒ 10% of x = x – 22500
⇒ 22500 = 0.90x
⇒ x = Rs. 25000
∴ Profit = marked price – cost price = 28125 – 25000 = Rs. 3125 = 3125/25000 = 12.5% profit
4. A dishonest dealer professes to sell his goods at cost price but uses a weight of 960 g for a kg weight. Find his gain percent.
A. 4.12%
B. 4.16%
C. 4.33%
D. 5%
E. 6.22%
Solutions
Let cost price of 1 g goods = Rs. 1
Cost price of 960 g goods = Rs. 960
He used 960 g weight for 1 kg, so his Selling price = Rs. 1000
And C.P = Rs. 960
Error = 1000 – 960 = Rs. 40
We know,

5.A toy shop owner marks a toy car up by 50% and then offers a discount on this marked price. If the final selling price after the discount results in the owner making no profit or loss, what was the percentage discount offered by the owner?
A. 60%
B. 40%
C. 33.3%
D. Depends on the cost price
E. None of the above
Solutions
Let the assume the Cost price of the toy car be = CP = Rs. 100
We know that the toy shop owner made no profit no loss on selling this item
∴ Selling price of the toy car = SP = Cost price of the toy car = Rs. 100
Also marked price = MP = CP + 50 % of CP
MP = 100 + × 100 = Rs. 150
Discount = MP – SP = 150 – 100 = Rs. 50
Also, we know that the discount is calculated on the marked price.
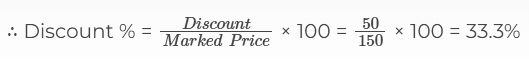
6. Two successive discounts of 10% and 20% is being offered on selling a refrigerator worth Rs. 88000. Find the selling price of the refrigerator?
A. Rs. 61200
B. Rs. 62400
C. Rs. 63360
D. Rs. 66000
E. None of these
Solutions
If successive discounts of a% and b% are offered on an article of price ‘X’, then the selling price of the article = X (1 – a%) (1 – b%)
Substituting the values in the given problem, we get 88000 (1 – 10%) (1 – 20%)
88000 × (1 – 0.1) × (1 – 0.2) = 88000 × 0.9 × 0.8 = 79200 × 0.8 = Rs. 63360∴ Selling Price = Rs. 63360
7. What would be the selling price of an article, if a shopkeeper allows two successive discounts of 10% each on the marked price of Rs. 120 ?
A. 96 Rs
B. 84 Rs
C. 97.2 Rs
D. 100 Rs
E. None of these
Solutions
When two discounts of 10% each are allowed on the marked price of Rs. 120:

8. Profit on selling 10 ceiling fans equal selling price of 3 coolers. While loss on selling 10 coolers equal selling price of 4 ceiling fans. Also profit percentage equals to the loss percentage and cost of a ceiling fan is half the cost of a cooler. What is the ratio of selling price of ceiling fan to the selling price of a cooler?
A. 5 ∶ 4
B. 3 ∶ 2
C. 4 ∶ 5
D. 3 ∶ 4
E. Data is insufficient
Solutions
Let the cost prices of ceiling fan and cooler be a and c respectively
Also, selling prices of ceiling fan and cooler be b and d respectively
ATQ,
⇒ c = 2a
Also,
⇒ Profit = 10(b – a) = 3d
⇒ Loss = 10(c – d) = 4b
So,
⇒ Profit% = (3d/10a) × 100
⇒ Loss% = (4b/10c) × 100
Again, given that,
⇒ (3d/10a) × 100 = (4b/10c) × 100
⇒ 3d/a = 4b/c
⇒ 3d/a = 4b/2a
⇒ b/d = 3/2∴ Required ratio is 3 ∶ 2
9. Mr. Harish bought 50 dozen mangoes at Rs. 20 a dozen. He spent Rs. 500 on transportation. He sold them at Rs 2 each. What was his profit or loss percent?
A. Loss 20%
B. Gain 20%
C. Loss 15%
D. Gain 15%
E. None of these
Solutions
C.P of 1 dozen mangoes = Rs. 20
C.P of 50 dozen mangoes = 50 × 20 = Rs. 1000
Final C.P of 50 dozen mangoes including transportation = Rs. 1000 + 500 = Rs. 1500
S.P of 1 mango = Rs. 2
Total number of mangoes in 50 dozen = 50 × 12 = 600 mangoes
S.P of 50 dozen mangoes = Rs. 600 × 2 = Rs. 1200
Loss = C.P – S.P = 1500 – 1200 = Rs. 300
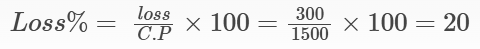
10. A grocer purchased 14 kg of rice at the rate of Rs. 28 per kg and 26 kg of rice at the rate of Rs. 19 per kg. If he sold the mixture at Re. 26 per kg , find the profit in this sale?
A. Rs. 154
B. Rs. 186
C. Rs. 224
D. Rs. 174
E. None of these
Solutions
C.P. of 40 kgs of mixture = Rs. (14 × 28 + 26 × 19) = Rs. 886
S.P. of 40 kgs of mixture = Rs. (40 × 26) = Rs. 1040∴ Profit = 1040 – 886 = Rs. 154
11. Two sports bikes were sold for Rs. 18,750 each, gaining 25% on one and losing 25% on the other. The gain or loss percent on the whole transaction is
A. Neither loss nor gain
B. 6% profit
C. 7 1/4 % profit
D. 6 % loss
E. None of these
Solutions
Let the two sports bikes be A & B.
Total S.P. of the two sports bikes = 18750 × 2 = Rs. 37,500
C.P. of sports bike A (C.P1) = S.P. of sports bike A – Profit
⇒ C.P1 = 18750 – (25% of C.P1)
⇒ C.P1 + 0.25 C.P1 = 18750
⇒ C.P1 = 18750/1.25 = Rs. 15,000
∴ C.P. of sports bike A = C.P1 = Rs. 15,000
C.P. of sports bike B (C.P2) = S.P. of sports bike B + Loss
⇒ C.P2 = 9900 + (25% of C.P2)
⇒ C.P2 – 0.25C.P2 = 18750
⇒ C.P1 = 18750/0.75 = Rs. 25,000
∴ C.P. of sports bike B = C.P2 = Rs.25,000
C.P. of the two sports bikes = 15000 + 25000 = Rs. 40,000
∵ S.P. of the whole transaction < C.P. of the whole transaction, there is loss.
∴ Loss % on the whole transaction

12. Directions: The following question is accompanied by three statements I, II and III. You have to determine which statements(s) is/are sufficient/necessary to answer the questions.
An article is sold at some price. Find the percentage gain?
I. lf the article had been sold for Rs. 150 less, there would have been no profit or loss
II. Had the article been sold for Rs. 50 more, the gain would have been 20%III. The cost price of the article is Rs. 1000
A. Only I or III
B. Any one of them
C. III and either I or II
D. Any two of them
E. None
Solutions
By statement I,
We can assume that the selling price is Rs. x
If the selling price was Rs. 150 less, there would be no profit or loss
So, cost price of article = selling price – 150 = Rs. x – 150
From statement II,
If the selling price was Rs. 50 more, the profit would be 20%
Therefore, new selling price would be x + 50
Based on statement I and statement II,
Profit = selling price – cost price = (x + 50) – (x – 150) = Rs. 200
⇒ x – 150 = 1000 ⇒ x = Rs. 1150
Profit % = (150/1000) × 100 = 15%
Similarly, if statement III is given with any of the other two, the profit % can be calculated.∴ Any two statements are enough.
13. Given below is a question and two statements numbered I and II given below it. You have to decide whether the data provided in the statements is sufficient to answer the question. You should use the given data and your knowledge of Mathematics to choose between the possible answers.
What is the cost price of a bicycle?
I. The profit earned in selling the bicycle is Rs. 550.
II. If the bicycle were sold for Rs. 500, the loss would have been 30%.
A. The data in statement I alone is sufficient to answer the question, while the data
B. The data in statement II alone is sufficient to answer the question
C. The data in statement I alone or in statement II alone is sufficient to answer the question
D. The data in both the statements I and II is not sufficient to answer the question.
E. The data in both the statements I and II together is necessary to answer the question.
Solutions
From statement I:
Knowing only the amount of profit, cost price cannot be found.
∴ Statement I alone is not sufficient to answer the question.
From statement II:
If the bicycle were sold for Rs. 500, the loss would have been 30%.
Here we know that selling price is Rs. 500, and loss is 30%. We can find the cost price using the equation,

∴ Statement II alone is sufficient to answer the question.
14. Given below are two quantities named A and B. Based on the given information, you have to determine the relation between the two quantities. You should use the given data and your knowledge of Mathematics to choose among the possible answers.
Find the profit percentage.
Quantity A: Cost price of 20 apples is equal to selling price of 15 apples.Quantity B: Cost price of 20 apples is Rs.100 each, labors cost is 500 and salaries paid is around 250 then apple is sold at Rupees 150 each.
A. Quantity A > Quantity B
B. Quantity A ≥ Quantity B
C. Quantity B > Quantity A
D. Quantity B ≥ Quantity A
E. Quantity A = Quantity B or Relation cannot be established
Solutions
Quantity A
⇒ 20 × Cost price = 15 × Selling price
⇒ Cost price/Selling price = 15/20
⇒ 1 – Cost price/Selling price = 1 – 15/20
⇒ (Selling price – Cost price)/Selling price = (20 – 15)/20
⇒ Profit/Selling price = 5/20
Required profit %
⇒ 5/15 × 100 = 33.33%
Quantity B
Total cost price = 20 × 100 + 500 + 250 = 2750
Total selling price = 150 × 20 = 3000
Profit % = (3000 – 2750)/2750 × 100
⇒ 9.08%∴ Quantity A > Quantity B
15. Given below are two quantities named A and B. Based on the given information, you have to determine the relation between the two quantities. You should use the given data and your knowledge of Mathematics to choose between the possible answers.
Quantity A: By how much percentage a shopkeeper must mark the goods above the cost price so as by giving 20% discount, he can still earn 8% profit?Quantity B: 30%
A. Quantity B > Quantity A
B. Quantity B < Quantity A
C. Quantity B ≥ Quantity A
D. Quantity B ≤ Quantity A
E. Quantity B = Quantity A
Solutions
First, we will find Quantity A
Quantity A:
Suppose the cost price = Rs. x
∴ Selling price = 1.08x
Since 20% discount is given;
∴ Marked price = 1.08x/0.8 = 1.35x
∴ The goods must be marked 35% above the cost price.
Now,
Quantity B: 30%∴ Quantity B < Quantity A
