1.A shopkeeper bought sugar and rice at Rs. 30 and Rs. 50 per kg respectively and is selling them by increasing the price by Rs. 10 per kg. He also has 5 faulty weights of 1 kg each and of equal weight. When a man bought 4 kg of rice and 5 kg of sugar from him, he made an overall profit of 28%. What is the actual weight of his 1 kg faulty weight?
A. 976 g
B. 982 g
C. 987 g
D. 991 g
E. 994 g
Solutions
Let the actual weight of the 1 kg faulty weight be ‘x’ kg
Quantity of rice he gave the man = 4x
Quantity of sugar he gave the man = 5x
Cost price of the products he gave the man = 50 × 4x + 30 × 5x = 200x + 150x = 350x
Selling price of 1 kg sugar = 30 + 10 = Rs. 40
Selling price of 1 kg rice = 50 + 10 = Rs. 60
Selling price of the products he gave the man = 60 × 4 + 40 × 5 = 240 + 200 = Rs. 440
Now, profit earned = selling price – cost price = 28% of cost price
⇒ 440 – 350x = 0.28 × 350x
⇒ 440 = 98x + 350x
⇒ x = 440/448 = 0.982 kg∴ The actual weight of 1 kg faulty weight is 982 g
2. A dishonest shopkeeper makes cheating of 10% at the time of buying and 10% at the time of selling the goods. He says of selling the goods at 10% loss. Find his profit percent(Approx.).
A. 7.5%
B. 9%
C. 10%
D. 11%
E. 12.3%
Solutions
Let cost price of 1 gm goods = Rs. 1
Let the shopkeeper purchases 100 gm goods.
Total cost price = Rs. 100
Due to cheating he actually gets = 100 + (10/100) × 100 = 110 gm goods.
Due to cheating at the time of selling the goods, he sells = 100 – 10 × (10/100) = 90 gm goods
According to the question,
He is selling the article at the loss of 10%
Selling Price = 100 – (10/100) × 100 = Rs 90
Actually the shopkeeper is selling 90 gm of article at Rs 90Required profit percentage = (10)/100 × 100 = 10%
3. Jabong, an online shopping site announces a sale. It offers flat 50% on the marked price. However those customers who pay using PayTm wallet are offered 10% extra discount. The customers have to pay 2% as service tax for paying through PayTM. Ankit buys a Watch labeled at Rs. 56789 using PayTm. How much Ankit has to pay for it?
A. Rs. 26066.15
B. Rs. 25043.95
C. Rs. 20444.04
D. Rs. 31943.81
E. None
Solutions
After the successive discounts of 50% and 10%,
Sell Price = Rs. (56789 × 0.50 × 0.9) = Rs.25555.05
After using PayTM wallet and paying 2% service tax,
Sell Price = Rs. 25555.05 (1 + 0.02) = Rs 26066.151∴ Ankit has to pay Rs. 26066.151 for the watch.
4. Two electronic musical instruments were purchased for Rs. 8000. The first was sold at a profit of 40% and the second loss of 40%. If the sale price was the same in both the cases. What was the cost price of two electronic musical instruments?
A. Rs.2000, Rs.5000
B. Rs.2200, Rs.5500
C. Rs.2400, Rs.5000
D. Rs.2400, Rs.5600
E. None of these
Solutions
Given that the two electronic musical instruments were purchased for Rs.8000
Let us assume that the cost prices of first and second musical instruments are `x’ and `y’ respectively.
⇒ x + y = Rs. 8000 ……………….. (1)
It is also mentioned that the selling price of both the instruments is same
Given that the first instrument was sold at a profit of 40%
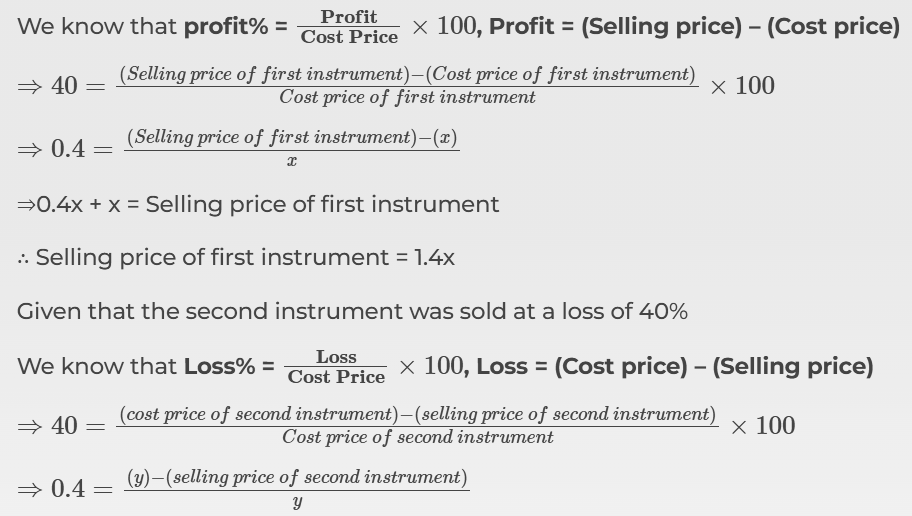
⇒0.4y = y – (Selling price of second instrument)
∴ Selling price of second instrument = y – 0.4y = 0.6y
∴ 1.4x = 0.6y (∵selling prices of both the instruments is same)
⇒ x = (3y/7) ………………….. (2)
By substituting (2) in (1), we get
⇒ (3y/7) + y = 8000
⇒ (10y/7) = 8000
∴ y = 8000 × (7/10) = Rs.5600
∴ x = (3/7) × 5600 = Rs.2400∴ The cost prices of first and second electronic musical instruments are Rs.2400 and Rs.5600 respectively
5. An article costing Rs. 20 was marked 25% above the cost price. After two successive discounts of the same percentage, the customer now pays Rs. 20.25. What would be the percentage change in profit had the price been increased by the same percentage twice successively instead of reducing it?
A. 3600%
B. 3200%
C. 2800%
D. 4000%
E. None of these
Solutions
Cost price of the article = 20
Selling price = 20.25
So, profit = 20.25 – 20 = 0.25 Rs
Let, the successive discount percentage is x.
The mark price of the article was 25% greater than its cost price.
Mark price = 20 + (25/100) × 20 = 25 Rs.

6. A discount of 20% is given by a shopkeeper on an article. He also charged an additional amount of _________% on the amount which is given as discount and sold the article for Rs. 1171.5. He sold the same article for Rs. 1349 after offering a discount of 5%.
A. 12.50%
B. 14%
C. 16.75%
D. 10.25%
E. None of these
Solutions
Let the MP of the article be Rs. y and additional charge be x%
SP of the article = Rs. 0.8y
Discount = Rs. 0.2y
Extra charge = x% of 0.2y
∴ SP of the article after extra charge = 0.8y + x% of 0.2y
0.8y + x% of 0.2y = 1171.5
Now, MP of the article y = 1349/0.95 = Rs. 1420
∴ 0.8 × 1420 + x% of 0.2 × 1420 = 1171.5
⇒ 1136 + x% of 284 = 1171.5
⇒ x% of 284 = 35.5⇒ x = 12.5%
Directions For Questions
7. Direction∶ A mobile phone is sold by a manufacturing company to the distributer at 25% profit at the manufacturing cost of the mobile and the same set is subsequently sold to a mobile store by the distributer after earning a profit of 12.5%. The mobile store then adds some accessories with the phone which cost Rs. 500 and sells the whole set to the customer at Rs. 14558.25. The customer after using the phone set for some time sold the phone to a mobile shop at 20% loss. The mobile shop owner marked the set at Rs. 13328.88 and sold the same phone to Kishor earning 3% profit after giving some discounts.
Find the percentage discount offered to Kishor by the mobile shop owner.
A. 5%
B. 15%
C. 10%
D. 8%
E. 7.5%
Solutions
∵ The 1st customer buys the set at Rs. 14558.25 and sells the set at 20% loss to the mobile shop;
∴ Cost price for the mobile shop = 14558.25 × 0.8 = Rs. 11646.6
The mobile shop owner marked the set at Rs. 13328.88 and sold the same phone to Kishor earning 3% profit after giving some discounts;
∴ Selling price of the set for the shop owner = 11646.6 × 1.03 = Rs. 11996
Suppose the discount percentage is y;
∴ 13328.88 = [11996 × 100]/(100 – y)
⇒ 100 – y = 1199600/13328.88
⇒ 100 – y = 90
⇒ y = 10∴ Percentage discount offered to Kishor = 10%
8. Directions For Questions
Direction∶ A mobile phone is sold by a manufacturing company to the distributer at 25% profit at the manufacturing cost of the mobile and the same set is subsequently sold to a mobile store by the distributer after earning a profit of 12.5%. The mobile store then adds some accessories with the phone which cost Rs. 500 and sells the whole set to the customer at Rs. 14558.25. The customer after using the phone set for some time sold the phone to a mobile shop at 20% loss. The mobile shop owner marked the set at Rs. 13328.88 and sold the same phone to Kishor earning 3% profit after giving some discounts.
If the cost price of whole set for the mobile store is Rs. 11750 and the mobile store applies 18% GST (Goods and Services Tax) on the price of the whole set after adding its profit, then what is the percentage profit earned by the mobile store on the whole set (Mobile + Accessories)?
A. 5%
B. 7.5%
C. 10%
D. 12.5%
E. 2.5%
Solutions
∵ The mobile store sells the whole set to the customer at Rs. 14558.25;
This price includes 18% GST ∶
∴ Price of the phone before 18% GST is applied = 14558.25/1.18 = Rs. 12337.5
∵ The cost price of the whole set = Rs. 11750
Suppose the profit percentage is x;
∴ 11750 × x/100 = 12337.5
⇒ x = 105%∴ The profit percentage earned by the mobile store on the whole set = 5%
9. Directions For Questions
Direction∶ A mobile phone is sold by a manufacturing company to the distributer at 25% profit at the manufacturing cost of the mobile and the same set is subsequently sold to a mobile store by the distributer after earning a profit of 12.5%. The mobile store then adds some accessories with the phone which cost Rs. 500 and sells the whole set to the customer at Rs. 14558.25. The customer after using the phone set for some time sold the phone to a mobile shop at 20% loss. The mobile shop owner marked the set at Rs. 13328.88 and sold the same phone to Kishor earning 3% profit after giving some discounts.
Find the cost price of the whole set (Mobile + Accessories) for the mobile store, if the raw material cost of 150 mobile phones is Rs. 10.8 lakhs and the processing cost of a mobile phone is Rs. 800. (Total manufacturing cost of the mobile = Raw material cost + Processing cost)
A. Rs. 11250
B. Rs. 12250
C. Rs. 11150
D. Rs. 11750
E. Rs. 11650
Solutions
First we need to determine the manufacturing cost of a mobile phone ∶
Given∶
The raw material cost of 150 mobile phones is Rs. 10.8 lakhs;
∴ Cost of Raw material of a mobile phone = 1080000/150 = 7200
Given ∶ Processing cost of a mobile phone is Rs. 800;
∵ Total manufacturing cost of the mobile = Raw material cost + Processing cost;
∴ Manufacturing cost of a mobile phone = 7200 + 800 = Rs. 8000
∵The manufacturing company sells the phone at 25% profit to the distributor and the distributor sells the phone at 12.5% profit to the store;
∴ Cost price of the mobile phone for the mobile store = 8000 × 1.25 × 1.125 = Rs. 11250
∵ The cost of accessories is Rs. 500 which the mobile store adds with the phone;∴ Cost price of the whole set (Mobile + Accessories) for the mobile store = 11250 + 500 = Rs. 11750
10. Given below are two quantities A and B. Based on the information, you have to determine the relation between the two quantities. You should use the given data and your knowledge of mathematics to choose between the answers.
In the two situations below, find x and y
Quantity A: A t-shirt was being sold after giving two consecutive discounts of 12% and 20% for Rs. 550. What was the marked price ‘x’?
Quantity B: A t-shirt of marked price Rs. 860 was sold after two consecutive discounts of 5% and 18%. What is the selling price ‘y’?
A. Quantity A > Quantity B
B. Quantity A < Quantity B
C. Quantity A ≥ Quantity B
D. Quantity A ≤ Quantity B
E. Quantity A = Quantity B or No relation
Solutions
To find x
Selling price = Rs. 550
Discount 1 = 12% and discount 2 = 20%
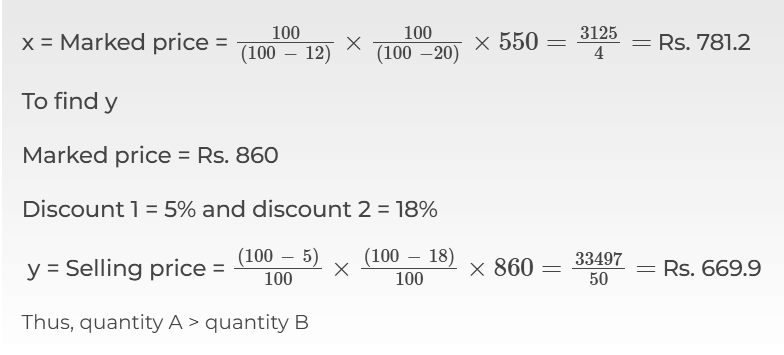
11. Under a scheme, a dealer sells a pack of 4 soaps of Jaali brand at a price equal to combined price of three soaps. How much percentage shall he increase the marked price of each soap so that he does not suffer any loss:
A. 12.5%
B. 25%
C. 33.33%
D. 50%
E. 66.67%
Solutions
Let the original price of soap be x
Actual price of pack = 4x
Let the soap be marked up by y%
New price of soap = x + (y/100) × x
New price of pack = 3(x + (y/100) × x)
As the price does not change, it should be equal to 4x
4x = 3(x + (y/100) × x)
4/3 = 1 + (y/100)y = 33.33%
12. Ebay offers the following discount plans for buyers of electronic goods
Plan 1: successive discount of 15% and 20%
Plan 2: discount of 14% followed by other discount of 21%
Plan 3: two successive discount of 10% and 25%
Plan 4: two successive discount of 18%The selling price will be least under which Plan?
A. Plan 1
B. Plan 2
C. Plan 3
D. Plan 4
E. None
Solutions
Let the marked price be Rs. x.
Sell Price = Marked Price (1 − Discount %)
Selling Price in Plan 1 = (1 – 0.15) × (1 – 0.20) × x = 0.68x
Selling Price in Plan 2 = (1 – 0.14) × (1 – 0.21) × x = 0.6794x
Selling Price in Plan 3 = (1 – 0.10) × (1 – 0.25) × x = 0.675xSelling Price in Plan 4 = (1 – 0.18) × (1 – 0.18) × x = 0.6724x
13. A shopkeeper wants to make some profit by selling wheat. He contemplates about various methods. Which of the following would maximise his profit?
I. Sell wheat at 15% profit.
II. Use 850 g of weight instead of 1 kg.
III. Mix 15% impurities in wheat and selling wheat at cost price.
IV. Increase the price by 7.5% and reduce weights by 7.5%.
A. II
B. III
C. IV
D. Profit is same
E. None of these
Solutions
Let the CP of 1 kg of wheat be Rs. 100
Then CP of 850 g of rice = (100/1000) × 850 = Rs. 85
Hence, profit % in case II = [(100 – 85)/85] × 100 = 17.65%
If he adds 15% impurities then his CP for 1 Kg = (100/1150) × 1000 = Rs. 86.95
Hence, profit % in case III = ((100 – 86.95)/86.95) × 100 = 15.01%
If he reduces weight by 7.5% then,
cost price of 925 g = (100/1000) × 925 = Rs. 92.5 and SP = Rs. 107.5
∴ Profit % in case IV = ((107.5 – 92.5)/92.5) × 100 = 16.22
Hence, the answer is option 1.
14. The Maximum Retail Price (MRP) of a product is 55% above its manufacturing cost. The product is sold through a retailer, who earns 23% profit on his purchase price. What is the profit percentage (expressed in nearest integer) for the manufacturer who sells his product to the retailer? The retailer gives 10% discount on MRP.
A. 31%
B. 22%
C. 15%
D. 13%
E. 11%
Solutions
Let the manufacturing cost = 100
The MRP of the product = 100 + 55% of 100 = 155
So, the retailer sells the product at 155 – 10% of 155 = 155 – 15.5 = 139.5
The retailer makes a 23% profit on his purchase price
Let the purchase price for the retailer be x
So, the retailer sells the product at x + 23% of x = 123% of x
Retailer sells the product at 139.5 = 123% of x
1.23x = 139.5
⇒ x = 139.5/1.23
⇒ x = 113.41
Cost to the manufacturer is 100
Profit made = 113.4 – 100 = 13.4
Profit made by the manufacturer is 13.4%. = 13% (nearest integer)
∴ Profit made by the manufacturer is 13%
15. If a shop keeper allows a discount of 20% on the shirt priced Rs x. Due to the decreased sale, he further allows a discount of 20% on the shirt. As the sales of the shirt increased, he increased its market price by ‘y’ %. If the difference of the original marked price and selling price in all three cases are in the ratio 5 : 9 : 5, what is the value of y?
A. 35
B. 20
C.15
D. 25
E. 30
Solutions
Original marked price = x
⇒ Selling price after giving 20% discount = (100 – 20)/100 × x = 0.8x
⇒ Difference between original marked price and selling price = x – 0.8x = 0.2x
⇒ Selling price after giving further 20% discount = (100 – 20)/100 × 0.8x = 0.64x
⇒ Difference between original marked price and selling price = x – 0.64x = 0.36x
⇒ Selling price after increasing the price by y%:-
⇒ (100 + y)/100 × 0.64x = (1 + 0.01y)× 0.64x = 0.64x + 0.0064xy
⇒ Difference between original marked price and selling price:-
⇒ x – 0.64x – 0.0064xy = 0.36x – 0.0064xy
Given, they are in the ratio, 5 : 9 : 5
⇒ 0.2x /(0.36x – 0.0064xy) = 5/5 =1
⇒ 0.2x = 0.36x – 0.0064xy
⇒ 0.0064xy = 0.16x
⇒ y = 0.16/ 0.0064 = 25∴ y = 25
