1. The monthly salary of Vinay and Ishit is in the ratio of 5 : 7. From Vinay’s salary, 1/4th amount is paid for loan, he gives 1/3rd of the remaining amount to his wife, donates 25% to NGO and invests 30% in mutual funds. At the end Vinay is left with Rs. 4,500 as savings. What is the approximate % of difference between Vinay and Ishit salary with respect to Ishit’s salary?
A. 21%
B. 29%
C. 32%
D. 37%
E. 41%
Solutions
Ratio of salary of Vinay and Ishit = 5 : 7
Amount remaining as savings with Vinay after all the spending = Rs. 4500
Let Vinay’s salary = Rs. x
Amount remaining after paying the loan = x – (1/4)x = x – 0.25x = 0.75x
Expenses from remaining amount
⇒ [(1/3) × 0.75x] + [(25/100) × 0.75x] + [(30/100) × 0.75x]
⇒ 0.25x + 0.1875x + 0.225x
⇒ 0.6625x
So, Savings = 0.75x – 0.6625x = 0.0875x
Given that, Savings = 4500
⇒ 4500 = 0.0875x
⇒ Salary of Vinay = x = (4500/0.0875) = Rs. 51428.57 = Rs. 51429 (approximately)
Given salary of Vinay : Ishit = 5 : 7
Salary of Ishit = Salary of Vinay × (7/5) = 51429 × (7/5) = 10285.8 × 7 = Rs. 72000.6 = Rs. 72001 (approximately)
Difference in salary = 72001 – 51429 = Rs. 20572
% Difference with respect to Ishit’s salary = (20572/72001) × 100 = 28.57% = 29% (approx.)∴ Required Percentage = 29%
2. An x litres solution contains x% acid. If y litres of water is added to the solution to reduce the acid percentage to (x – 10)%, determine the value of y.
A. x2/100
B. 10x/(x – 10)
C. 10x/(x + 10)
D. 10x2/(x – 10)
E. 10x2/(x + 10)
Solutions
x litres of solution of x% acid
⇒ x/100 × x = x2/100 acid in solution (1)
New solution = x + y litres
% of acid = [(x2/100)/(x + y)] × 100 = x – 10
x2/(x + y) = x – 10
x2 = x2 – 10x + xy – 10yy = 10x/(x – 10)
3. The ratio of Uday’s salary for January to his salary for February was 2.5 ∶ 2.333 and the ratio of the salary for February to that of March was 3 ∶ 3.6666. The worker got 114 rupees more for March than January and received a bonus constituting 40% of the salary for three months. Find the bonus. Assume that the number of workdays is the same in every month.
A. 1096
B. 996
C. 1196
D. 896
E. 1000
Solutions
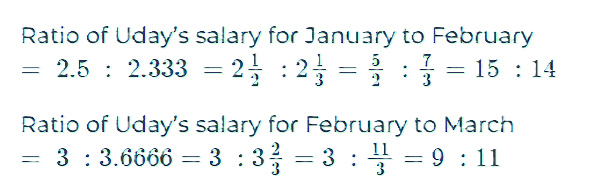
Ratio of Uday’s salary for January to February to March = 135 ∶ 126 ∶ 154
Let the salary of Uday in January be 135x, February be 126x and March be 154x
According to question,
⇒ Difference between salary in March and January = 154x – 135x = 19x
⇒ 114 = 19x
⇒ x = 114/19 = 6
⇒ Total salary of three months = 135x + 126x + 154x = 415x = 415 × 6 = Rs. 2490∴ Bonus = 40% of total salary of three months = 0.40 × 2490 = Rs. 996
4. An ugly spat between two sons of a business tycoon led to the division of the company into 2 pieces. While the elder son got hold of the 45% of the stake in the company and 5.5 billion dollars worth assets, the younger son gets 3.5 billion dollars worth of the assets and the leftover stake in the company. If the current value of the stakes is 30 billion dollars, which son is richer and by how much?
A. Elder son is richer by 1 billion dollars
B. Younger son is richer by 1 billion dollars
C. Elder son is richer by 2 billion dollars
D. Younger son is richer by 2 billion dollars
E. None of these
Solutions
Let us evaluate the individual net worth of the sons according to the current valuation of the stakes
Elder Son net worth:
Net worth = Stake + Assets
⇒ Net worth= 45% of the total stakes + Asset
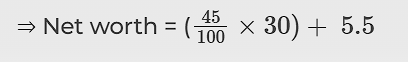
⇒ Net worth = 13.5 + 5.5
⇒ Net worth = 19 billion dollars
Younger Son net worth:
Net worth = Stake + Assets
⇒ Net worth= 55 % of the total stakes + Asset
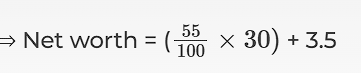
⇒ Net worth = 16.5 + 3.5
⇒ Net worth = 20 billion dollars∴ Younger son is richer by 1 billion dollars.
5.A natural number P is increased successively 3 times by 12% to obtain Q. The smallest number which must be multiplied by Q to get a natural number is 5. What will be the minimum value of P?
A..15625
B. 62500
C. 12500
D. 125000
E. 3125
Solutions
A natural number P is increased successively 3 times by 12% to obtain Q.
⇒ Q = P × (1 + 12/100) × (1 + 12/100) × (1 + 12/100) = 1.404928P
The smallest number which must be multiplied by Q to get a natural number is 5.
So, 7.02464P should be a natural number.
Checking options:
The smallest value of P for which it becomes a natural number is 3125.
7.02464P = 7.02464 × 3125 = 21952
6. The price of an item increases by T% every day. It takes a minimum of 4 days, so that the price became just more than twice of original price. What could be the value of T?
A. 15
B. 21
C. 30
D. 32
E .18
Solutions
Price after 4 days = Original price × (1 + T/100)4
Now, Original price × (1 + T/100)4 > 2 × original price
Also, price does not become more than double in 3 days.
⇒ (1 + T/100)4 > 2 > (1 + T/100)3
Among given options, only 21 satisfy this equation.So, T = 21.
7. Quantity A: A is 75% of B then what % of A is B?Quantity B: Isaac scores 73 marks in Mathematics, 98 marks in Physics and 75 in Chemistry. If the maximum marks in Mathematics, Physics and Chemistry are 75, 100, 90 respectively. What will be the % of total marks obtained with respect to the sum of maximum marks of Mathematics and Chemistry?
A. Quantity A > Quantity B
B. Quantity A < Quantity B
C. Quantity A ≥ Quantity B
D. Quantity A ≤ Quantity B
E. Quantity A = Quantity B
Solutions
First we will find Quantity A,
Quantity A:
A = 75% of B
⇒ A = 0.75B
⇒ B = A/0.75 = 1.33A = 133.33% of A
∴ B = 133.33% of A
Now,
Quantity B:
Sum of maximum marks of Mathematics and Chemistry = 75 + 90 = 165
Total marks obtained by Isaac = 73 + 98 + 75 = 246
Percentage of total marks obtained with respect to the sum of maximum marks of Mathematics and Chemistry = (246/165) × 100 = 149.09%
∴ Percentage of total marks obtained with respect to the sum of maximum marks of Mathematics and Chemistry = 149.09%∴ Quantity A < Quantity B
8.

A. Chikara has more pencils than Priya
B. Priya has more pencils than Chikara
C. They both have same number of pencils
D. Data insufficient
E. None of these
Solutions
Let Priya has 100 pencils initially, therefore no of pencils with Chikara = 140 (40% more).
Now,
| Chikara | Priya | |
| Initially | 140 | 100 |
| After 2 days | 120% of 140 = 168 | 90% of 100 = 90 |
| After 4 days | (2/3) of 168 = 112 | 90 + (1/3)× 90 = 120 |
We know that:
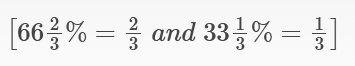
i.e. Priya has more pencils than Chikara.
9. If numerator of a fraction is increased by 240% and the denominator is increased by 180%, the resultant fraction is 1/2. What is the original fraction?
A. 1/13
B. 7/17
C. 1/9
D. 2/7
E. None of these
Solutions
Let the original fraction = x/y, then according to the question,

10. In the upcoming election of 2019, the forecasted report by KPMG is as follows.
a. Congress – 35% of valid votes
b. BJP – 65% of valid votes
c. Total no. of votes = 950000
d. Invalid votes = 30%If the above mentioned forecasted report will be 100% true, then calculate by how much percentage BJP will win considering only valid votes from total votes?
A. 91.42%
B. 89.73%
C. 85.71%
D. 93.23%
E. None of the above
Solutions
Total no. of votes = 950000
Total no. of valid votes = 0.7 × 950000 = 665000
No. of votes polled by Congress = 0.35 × 665000 = 232750
Total no. of Valid votes polled by BJP = 0.65 × 665000 = 432250∴ BJP won by congress by = (432250 – 232750)/232750 × 100 = 85.71 %
11. In Bengaluru, only two newspapers The Hindu and The Times of India are published. It is known that 25% of the city population reads The Hindu and 20% reads The Times of India while 8% reads both the newspapers. It is also known that 30% of those who read The Hindu but not The Times of India look into advertisement and 40% of those who read The Times of India but not The Hindu look into advertisement while 50% of those who read both the newspapers look into advertisements. What is the percentage of the population who read an advertisement?
A. 13.9%
B. 15.8%
C. 17.2%
D. 21.4%
E. None of these
Solutions
Let the population of the city be 100. Then,
People reading The Hindu = 25
People reading The Times of India = 20
People reading both = 8
People reading only The Hindu = 17
People reading only The Times of India = 12
Therefore, required percentage of people who read an advertisement = (5.1 + 4.8 + 4) = 13.9%.
12. A man gave 20% of his salary to his only son and only daughter. The ratio of amount given to son and daughter is 3 : 2 respectively. Twice the amount what he gave to his daughter, he invested in LIC. Out of the remaining amount he gave one-fourth to his wife. After that he was left with Rs. 16800. Find out the amount invested in LIC.
A. Rs. 5600
B. Rs. 5400
C. Rs. 5800
D. Rs. 6200
E. Rs. 6940
Solutions
Let the amount be ‘x’
⇒ 0.2x given to son and daughter in the ratio 3 ∶ 2
⇒ 3y + 2y = 0.2x
⇒ 5y = 0.2x
⇒ y = 0.2x/5 = 0.04x
∴ Amount given to son = 3 × 0.04x = 0.12x
Amount given to daughter = 2 × 0.04x = 0.08x
⇒ Amount invested in LIC = 2 × 0.08x = 0.16x
Remaining amount = x – 0.2x – 0.16x = 0.64x
∴ Amount given to wife = 0.64x/4 = 0.16x
⇒ 0.64x – 0.16x = 16800
⇒ 0.48x = 16800
∴ Total Salary = 16800/0.48 = 35000∴ Amount invested in LIC = 0.16x = 0.16 × 35000 = Rs. 5600
13. The net sales of an organization in year 2013 is ‘X’. Net sales decrease by 20% in 2014 and increase by 40% in 2015 as compared to the sales in previous years. If the variation in sales in 2016 is equal to the average variation in 2014 and 2015, then find the sales in 2016 in terms of X.
A. 1.06X
B. 1.12X
C. 1.18X
D. X
E. 1.1X
Solutions
Net sales in 2013 = X
Net sales in 2014 = 20% less than sales in 2013 = 0.8 × X
Variation in 2014 = Net sales in 2014 – Net sales in 2013 = -0.2 × X
Net sales in 2015 = 40% more than sales in 2014 = 1.4 × 0.8 × X = 1.12 × X
Variation in 2015 = Net sales in 2015 – Net sales in 2014 = 1.12X – 0.8X = 0.32X
Variation in 2016 = (Variation in 2014 + Variation in 2015)/2 = (-0.2X + 0.32X)/2 = 0.12X/2 = 0.06XNet sales in 2016 = Net sales in 2015 + Variation in 2016 = 1.12X + 0.06X = 1.18X
14. In a company, 20% of the total employees are in the top management and 35% are in middle management. If 24 middle management employees get promoted to top management, there will be 22% of total employees in top management. How many employees are there in the company?
A. 880
B. 1000
C. 1200
D. 1440
E. 2400
Solutions
Suppose there are T employees in company. If 24 middle management employees get promoted to top management, there will be 22% of total employees in top management instead of 20%.
⇒ 24 represents 2% employees of company.
⇒ 24 = T × (2/100)
⇒ T = 2400/2 = 1200∴ There are 1200 employees in company.
15. If Rajeev’s monthly income is 20% less than that of Raghu and Raghu’s monthly income is 25% less than that of Rannvijay, then find the difference between Rajeev and Rannvijay’s Annual income (in Rs.). Given that Raghu’s monthly income is Rs. 60000.
A. 32000
B. 384000
C. 80000
D. 240000
E. 144000
Solutions
Let Rannvijay’s monthly income be Rs. x.
∴ Raghu’s monthly income = x – (25% of x) = 0.75x
∴ Rajeev’s monthly income = 0.75x – (20% of 0.75x) = 0.6x
Difference between Rannvijay and Rajeev’s monthly income = x – 0.6x = 0.4x
∴ Difference between their annual income = 12 × 0.4x = 4.8x
Since Raghu’s monthly income = Rs. 60000
0.75x = 60000
x = 80000
∴ Difference between their annual income = 4.8 × 80000 = 384000
