1.A dealer sells a grain whose C.P is Rs. 50/kg at Rs 60/kg. First day by replacing it by a substitute of Rs. 40/kg and second day selling the pure grain. What is the ratio of profit % of the two days?
A. 1 : 2
B. 3 : 1
C. 3 : 2
D. 5 : 2
E. None of these
Solutions
C.P = Rs 40/kg
S.P = Rs. 60/kg

Alternative Method:
On day 1, CP: SP be = 2: 3
Profit = (1/2) × 100 = 50%
And on day 2, CP: SP be = 5: 6
Profit = (1/5) × 100 = 20%
∴ Required ratio = 5: 2
2. A man buys a single apple for Rs. 25. If he were to buy a dozen apples, he would have to pay a total amount of Rs. 250. What would be the approximate percent discount he would get on buying a dozen apples?
A. 45%
B. 33.33%
C. 25%
D. 22%
E. 17%
Solutions
According to the question,
Cost of one apple = Rs. 25
∴ Cost of 12 apples = 25 × 12= Rs.300
∴ Amount paid = Rs. 250
∴ Discount = 300 – 250 = Rs. 50
% Discount =

∴ The required answer is 17%,
3. A dishonest dealer sells as a weight of 800 gm in place of 1 kg and adds 25% impurities in sugar. What would be his profit % if he claims to be selling at cost price?
A. 50%
B. 56.25%
C. 45%
D. 66.25%
E. None of these
Solutions
[Formula: Two successive percentage change of a% and b% is an effective change of
= [a + b + (ab/100)%]
Dishonest dealer sells as a weight of 800 gm in place of 1 kg.
In 800 gm he is making a profit of (1kg – 800 gm) = 200 gm.
The percentage of profit he is making by this
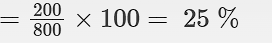
He adds 25% impurities in sugar.
Using the formula, two successive percentage change is happening on cost price. So total percentage change = [25 + 25 + 25 × (25/100)]% = 56.25%Hence the answer is 56.25%.
4. A shopkeeper purchased 150 apples for Rs. 10 each. However, 10 apples were rotten and had to be thrown away. The remaining were sold at Rs. 15 each. What will be the percentage profit?
A. 20 %
B.50 %
C. 30 %
D. 40 %
E. None of these
Solutions
⇒ cost price = 150 × 10 = 1500 rupees
10 apples were rotten and had to be thrown away.
So, 140 apples are remaining.
⇒ selling price of 140 apples = 140 × 15 = 2100 rupees
⇒ profit = selling price – cost price = 2100 – 1500 = 600 rupees
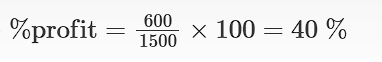
5. There are three partners A, B and C in a business, and each had a share of the profits in proportion to his capital. A’s share in profit was Rs. 300; B’s Rs. 400; and A’s share was Rs. 15 in every Rs. 100. Find the share in the profit of C.
A. Rs. 1230
B. Rs. 1650
C. Rs. 1680
D. Rs. 1720
E. Rs. 1300
Solutions
A gets Rs 15 out of Rs 100 as given in the question
∴ A’s share = 15/100 × profit amount
⇒ Profit amount = 100/15 × A’s share = 100/15 × 300 = Rs 2000
As A’s share is given to be Rs 300Such that C’s Profit = Profit amount – A’s Profit – B’s Profit = 2000 – 300 – 400 = 1300 Rs.
6. A man sells an article at 14 % profit. Had he bought it at 14 % less and sold it for Rs. 1424 less, he would have gained 16%. Find the cost price.
A. Rs. 10500
B. Rs. 10000
C. Rs. 9500
D. Rs. 5000
E. none of these
Solutions
Let the Cost price be Rs. x
∵ the article is sold at 14% profit,
Selling price = x + (14% of x) = 1.14x
Now, in the second case, the article was bought at 14% lesser value than the previous value
∴ Cost price in second case = x – (14% of x) = 0.86x
In the second case, the article was sold at a price Rs. 1424 less than the previous selling price.
∴ Selling price in second case = 1.14x – 1424
Now, Gain in the second case = (1.14x – 1424) – 0.86x

⇒ 16 × 0.86x = 100 × (0.28x – 1424)
⇒ 13.76x = 28x – 142400
⇒ 14.24x = 142400
⇒ x = 10000∴ Cost price of the article is Rs. 10000.
7. A shopkeeper sells a TV set on discount of 10% of print price and gains 20%. If print price was Rs. 15000, then what was the cost price?
A. Rs. 11800
B. Rs. 11250
C. Rs. 11500
D. Rs. 12720
E. None of these
Solutions
The print price = Rs. 15000
The selling price at 10% discount in print price = Rs. 15000 × (90/100) = Rs. 13500
He gains 20% selling the TV set at Rs. 13500.
We know that ,
Cost Price=[100/(100+ Gain %)]×Selling Price∴ The cost price was = Rs. 13500 × (100/120) = Rs. 11250
8. For an item, the profit percentage and the discount percentage is same. The cost price is Rs. 400 and marked price is Rs. 625. Find the selling price of this item. (in Rs.)
A. 441.9
B. 456.3
C. 467.9
D. 487.8
E. 496.2
Solutions
Let the profit percentage(or discount percentage be T%).
We know, Selling price = Marked price × (1 – discount percentage/100)
And, Selling price = Cost Price × (1 + Profit Percentage/100)
Equating we get,
625 × (1 – T/100) = 400 × (1 + T/100)
⇒ 625 – 6.25T = 400 + 4T
⇒ T = 225/10.25 = 21.95∴ Selling price = 400 × (1 + 21.95/100) = Rs. 487.8
9. The cost of 25 items is the same as the revenue earned by selling x items. Find x, if the profit made in the transaction is 25%.
A. 25
B. 16
C. 20
D. 32
E. 30
Solutions
Let the cost price of one item be Rs. A.
∴ Selling price to make 25% profit = A × 1.25 = 1.25 A
Since the cost of 25 items is the same as the revenue earned by selling x items;
∴ 25 × A = 1.25 A × x⇒ x = 20
10. Dishonest seller buys milk at the price of Rs. 23 per liter. He purchased the barrel of 20 liters. Before selling he mixed 5 liter of water in 20 liter mixture of milk. He sell the mixture at Rs. 20 per liter. The % of profit or loss is
A. 5.62% loss
B. 8.70% profit
C. 5.62% profit
D. 8.70% loss
E. None of the above
Solutions
Cost price per liter = Rs. 23
Purchased quantity = 20 liters
Total cost price = 23 × 20 = Rs. 460
Total volume of mixture prepared = 20 + 5 = 25 liter
Ratio of milk to water in mixture,
Mixture = 20 ∶ 5 = 4 ∶ 1
Amount of milk in 1liter,
Milk quantity = 1 × (4/5) = 0.8 liter
Selling price of 1 liter of milk = (20/0.8) = Rs. 25
Profit = 25 – 23 = Rs. 2∴ % of profit = (2/23) = 8.70%
11. Rajesh purchase a bag of 100 kg wheat at the price of Rs. 1850. If he sells the wheat at the price of Rs. 12.5 per kg, % of profit or loss would be.
A. 31.43% profit
B. 48% loss
C. 48% profit
D. 32.43% loss
E. None of the above
Solutions
Price of 100 kg wheat = Rs. 1850
Price of 1 kg of selling wheat = Rs. 12.5
⇒ Cost price of per kg wheat = 1850/100 = Rs. 18.5
Amount of loss = cost price – selling price
⇒ loss = 18.5 – 12.5 = Rs. 6
For % of loss,
⇒ % of loss = (6/18.5) × 100∴ % of loss = 32.43%
12. A company marked its product at a price that is 80% above its manufacturing price. With which of the following discount scheme will the company gain some profit?
A. Discount of 60%
B. Successive discounts of 40% and 20%
C. Successive discounts of 50% and 10%
D. Successive discounts of 30%, 20% and 10%
E. Successive discounts of 25%, 20% and 5%
Solutions
Let the manufacturing price of the product be Rs. ‘x’
Marked price = (100 + 80)% of x = 1.8x
Case 1: When discount of 60% is given,
Selling price = (100 – 60)% of 1.8x = 0.4 × 1.8x = 0.72x
As selling price is less than manufacturing price, there is no profit
Case 2: When successive discounts of 40% and 20% is given,
Selling price = (100 – 20)% of (100 – 40)% of 1.8x = 0.8 × 0.6 × 1.8x = 0.864x
As selling price is less than manufacturing price, there is no profit
Case 3: When successive discounts of 50% and 10% is given,
Selling price = (100 – 10)% of (100 – 50)% of 1.8x = 0.9 × 0.5 × 1.8x = 0.81x
As selling price is less than manufacturing price, there is no profit
Case 4: When successive discounts of 30%, 20% and 10% is given,
Selling price = (100 – 10)% of (100 – 20)% of (100 – 30)% of 1.8x = 0.9 × 0.8 × 0.7 × 1.8x = 0.91x
As selling price is less than manufacturing price, there is no profit
Case 5: When successive discounts of 25%, 20% and 15% is given,
Selling price = (100 – 5)% of (100 – 20)% of (100 – 25)% of 1.8x = 0.95 × 0.8 × 0.75 × 1.8x = 1.026x
As selling price is more than manufacturing price, there is some profit in this scheme∴ The company will gain some profit in giving successive discounts of 25%, 20% and 5%
13.A shopkeeper uses a faulty weight of 925 g instead of 1000 g. What will be his profit percentage?
A. 7.5%
B. 7.8%
C. 8.1%
D. 8.4%
E. 9%
Solutions
True weight = 1000 g
False weight = 925 g
Error = 1000 – 925 = 75 g
∵ Profit percentage = (error/false weight) × 100
∴ Profit % of shopkeeper = (75/925) × 100 = 8.1%
14. In the following question, two statements are numbered as A and B. On solving these statements we get quantities A and B respectively. Solve for the both quantities and choose the correct option.
Quantity A: A shopkeeper earned a profit of 11.5% on a product after selling it at a discount of 10%. At what percentage above the cost price did he marked the price of the product?Quantity B: A shopkeeper marked a product at 45% above its cost price. After selling it at a certain discount, he earns a profit of 15%. Find the discount percentage.
A. Quantity A > Quantity B
B. Quantity A < Quantity B
C. Quantity A ≥ Quantity B
D. Quantity A ≤ Quantity B
E. Quantity A = Quantity B
Solutions
Solving for Quantity A:
Let the cost price be Rs. ‘x’
Profit = 11.5% of x = 0.115x
Selling price = Cost price + profit = x + 0.115x = 1.115x
Now, Marked price – Discount = Selling price
⇒ MP – 10% of MP = 1.115x
⇒ 0.9MP = 1.115x
⇒ MP = 1.115x/0.9 = 1.24x
⇒ MP = (100 + 24)% of x
The marked price of the product is 24% above its cost price
⇒ Quantity A = 24%
Solving for Quantity B:
Let the cost price be Rs. ‘x’ and the discount be ‘d’%
Profit = 15% of x = 0.15x
Selling price = Cost price + profit = x + 0.15x = 1.15x
Marked price = (100 + 45)% of x = 1.45x
Now, Marked price – Discount = Selling price
⇒ 1.45x – d% of 1.45x = 1.15x
⇒ (d/100) × 1.45x = 1.45x – 1.15x
⇒ d = (0.3x/1.45x) × 100 = 20.7%
⇒ Quantity B = 20.7%∴ Quantity A > Quantity B
15. In the following question, two statements are numbered as A and B. On solving these statements we get quantities A and B respectively. Solve for the both quantities and choose the correct option.
Quantity A: A shopkeeper marked the price of a product at 40% above the cost price. If he gives a successive discount of 15%, 10% and 5% respectively on the product, find his profit percentage.Quantity B: A shopkeeper marked a product at a price 35% above its cost price and sold it by giving a discount of 25%. Find his profit percentage.
A. Quantity A > Quantity B
B. Quantity A < Quantity B
C. Quantity A ≥ Quantity B
D. Quantity A ≤ Quantity B
E. Quantity A = Quantity B
Solutions
Solving for Quantity A:
Let the cost price of the product be Rs. ‘x’
Marked price = (100 + 40)% of x = 1.4x
Selling price = (100 – 5)% of (100 – 10)% of (100 – 15)% of 1.4x = 0.95 × 0.9 × 0.85 × 1.4x = 1.01745x
Profit earned = 1.01745x – x = 0.01745x
Profit percentage = (0.01745x/x) × 100 = 1.745%
⇒ Quantity A = 1.745%
Solving for Quantity B:
Let the cost price of the product be Rs. ‘x’
Marked price = (100 + 35)% of x = 1.35x
Selling price = (100 – 25)% of 1.35x = 0.75 × 1.35x = 1.0125x
Profit earned = 1.0125x – x = 0.0125x
Profit percentage = (0.0125x/x) × 100 = 1.25%
⇒ Quantity B = 1.25%∴ Quantity A > Quantity B
